整数部分と小数部分
整数部分と小数部分とは
パン太先生
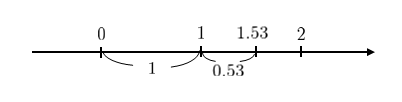
数は整数部分と小数部分からできています。例えば \(1.53\) は、整数部分が \(1\) 、小数部分が \(0.53\) となります。数直線で考えてみましょう。
パン太先生
\(1.53\) は \(1≦1.53<2\) なのが確認できますか?\(1.53\) が \(1\) 以上 \(2\) 未満ということは、整数部分は \(1\) となります。
うさこ
なるほど、数直線で見るとわかりやすいですね!
パン太先生
小数部分は \(1.53\) から整数部分の \(1\) を引いた \(0.53\) になります。一般的に、整数部分と小数部分を足すともとの数になります。
うさこ
さっきの例も、整数部分 \(1\) と小数部分 \(0.53\) を足すと、もとの数の \(1.53\) になりますね!
パン太先生
整数部分と小数部分には次の関係があるので確認しましょう。
(整数部分)+(小数部分)=(もとの数)
(小数部分)=(もとの数)ー(整数部分)
うさこ
小数部分を求めるには、もとの数から整数部分を引けばいいんですね!
パン太先生
そうですね、では練習として次の数の整数部分と小数部分を求めてみてください。
例) \(\sqrt {3}\) の整数部分と小数部分
うさこ
まず、\(\sqrt {3}\) がどの整数の間にあるかを考えたらよさそうですね。
うさこ
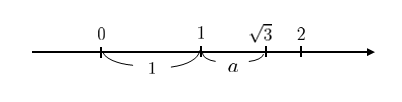
\(\sqrt {3}\) はおよそ \(1.73\) であるので、数直線上に表せますね。\(1≦\sqrt {3}<2\) なので整数部分は \(1\) になります!
パン太先生
そうですね、では小数部分はどうですか?数直線では \(a\) のことですね。
うさこ
小数部分はもとの数から整数部分を引いたら出るはずです!なので小数部分は \(\sqrt {3}-1\) になります!
パン太先生
よくできました。だいぶ慣れてきたところで整数部分と小数部分を使った問題を解いてみましょう。
練習問題
練習① \(\sqrt {17}\) の整数部分 \(a\) と、小数部分 \(b\) を求めよ。
うさこ
\(\sqrt {17}\) なんて、どの整数の間にあるかわかりませんよ。
パン太先生
少し工夫して考えてみましょう。\(1\) はルート何ですか?\(2\) はルート何?\(3\) は?このように順に考えてみると \(\sqrt {17}\) がどの整数の間にあるかが分かるはずです。
うさこ
やってみます!
\(1=\sqrt {1}\)
\(2=\sqrt {4}\)
\(3=\sqrt {9}\)
\(4=\sqrt {16}\)
\(5=\sqrt {25}\)
分かりました!\(\sqrt {17}\) は \(\sqrt {16}\) と \(\sqrt {25}\) の間なので、整数では \(4\) と \(5\) の間です!
パン太先生
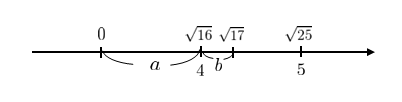
そうですね、数直線では次のようになります。
うさこ
\(4≦\sqrt {17}<5\) なので、整数部分 \(a\) は \(4\) になりますね!小数部分は、もとの数から整数部分を引けばよいので \(b=\sqrt {17}-4\) になります!
パン太先生
よくできました。試験問題などでは、整数部分 \(a\) 、小数部分 \(b\) を求めて与えられた式に代入する問題が出されます。1問練習しましょう。
練習② \(\frac {1}{\sqrt {2}-1}\) の整数部分を \(a\) 、小数部分を \(b\) とするとき、\(a^2+ab\) を求めよ。
パン太先生
解答を次に載せますので、練習と同じ要領で解いてみましょう。
解答
\(\frac {1}{\sqrt {2}-1}\)\(=\)\(\frac {\sqrt {2}+1}{(\sqrt {2}-1)(\sqrt {2} +1)}\)
\(=\sqrt {2}+1\)
\(1≦\sqrt {2}<2\) より、\(\sqrt {2}\) の整数部分は \(1\) 、
\(\sqrt {2}+1\) の 整数部分 \(a\) は、\(2\) となる。
また、\(b=(\sqrt {2}+1)-a\)
\(=(\sqrt {2}+1)-2\)
\(=\sqrt {2}-1\)
\(=(\sqrt {2}+1)-2\)
\(=\sqrt {2}-1\)
よって、\(a^2+ab=a(a+b)\)
\(=2(2+\sqrt {2}-1)\)
\(=2(\sqrt {2}+1)\)
\(=2\sqrt {2}+2\)
\(=2(2+\sqrt {2}-1)\)
\(=2(\sqrt {2}+1)\)
\(=2\sqrt {2}+2\)
パン太先生
しっかり理解していないと、やり方を忘れてしまったなんてことも多い問題なので、数直線の書き方もマスターしておきましょう。今回はこれで終わりになります。お疲れさまでした。


