因数分解 たすき掛け
たすき掛けとは
パン太先生
今回はたすき掛けについて勉強しましょう。
うさこ
たすきってよく駅伝で見るようなのですか?
パン太先生
ここでいうたすきは和服などでつけるたすきのことを言います。後ろを向いた姿のイメージはこんな感じです。
うさこ
なるほどぉ、クロスしているんですね!
パン太先生
はい、計算する際にこのたすきのように計算することから「たすき掛け」と呼ばれています。実際に計算の例を見ると実感できると思います。
たすき掛けのやり方
パン太先生
まずはじめに「たすき掛け」が使われる公式を紹介します。
\(acx^2+(ad+bc)x+bd=(ax+b)(cx+d)\)
うさこ
なんだかごちゃごちゃしてますね。
パン太先生
安心してください。しっかり説明していきますからね。では、1つ例を出してみます。
\(2x^2+7x+6\)
パン太先生
これとさっきの公式を比べてみましょう。
\(2x^2+7x+6=(ax+b)(cx+d)\)
\(=acx^2+(ad+bc)x+bd\)
\(=acx^2+(ad+bc)x+bd\)
パン太先生
式を比べると
\(ac=2\)
\(ad+bc=7\)
\(bd=6\)
になることが分かりますね。あとは \(a\) , \(b\) , \(c\) , \(d\) を求めたら答えが出ます。
うさこ
そんな簡単にできません!!
パン太先生
落ち着いてください。ここで活躍するのが「たすき掛け」なのです。ところで、因数分解の基本の話をしたとき和と積のどちらを先に考えると言ったか覚えてますか?
うさこ
たしか組み合わせが少ないから積を先に考えるんですよね?
パン太先生
そうですね。たすき掛けをするときも積である \(ac\) , \(bd\) の組み合わせを先に考えましょう。その \(ac\) と \(bd\) を使って \(ad+bc\) が出せます。次の図を見てみましょう。
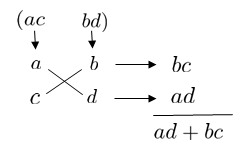
パン太先生
何をしているかと言いますと、
①\(ac\) と \(bd\) を分けます。
②\(a\) と \(d\) , \(c\) と \(b\) をそれぞれ掛けます。(たすき掛け)
③\(ad\) と \(bc\) を足します。
うさこ
たすき掛けをすると自然に \(ad+bc\) も見つかるんですね!
パン太先生
見つかるというよりは、自分で組み合わせを見つけると言った方が近いかもしれません。先ほどの例で考えてみましょう。
うさこ
まずは積の組み合わせですね!
\(ac=2\) は
\(2×1\) だけで
\(bd=6\) は
\(6×1\) , \((-6)×(-1)\)
\(3×2\) , \((-3)×(-2)\)
です!
パン太先生
そうですね。そして、\(ac\) の組み合わせは1つしかないので決まりです。では下の図の空欄に \(bd\) の組み合わせを入れてみましょう。
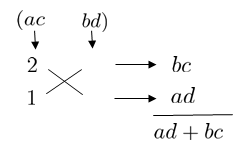
うさこ
\(bd=6×1\) の組み合わせを入れてみます!
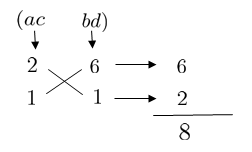
パン太先生
\(ad+bc\) が \(8\) になってしまいましたね。\(7\) にならなくてはなりませんので違いましたね。
うさこ
\(b\) と \(d\) を入れ替えてもだめそうです。
パン太先生
それでは次の組み合わせを入れてみてください。
うさこ
それじゃあ \(3\) と \(2\) を入れてみます。
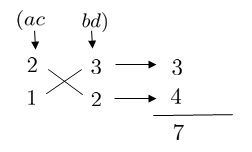
うさこ
先生!!\(7\) になりました!
パン太先生
よくできましたね。あとは因数分解の式を書いて完了です。
うさこ
どうやって因数分解の式を書いたらいいんですか??
パン太先生
公式を見ながら \(a\) , \(b\) , \(c\) , \(d\) に数字を入れてもいいですよ。もっと簡単な方法もあります。上の図のたすき掛けの横に並んでる同士をセットにします。上の図だと \(2\) と \(3\) , \(1\) と \(2\) です。それを踏まえると、
\((2x+3)(x+2)\)
になります。
うさこ
たすき掛けさえできればあとは簡単ですね!
たすき掛けをもっと速く
パン太先生
慣れてくると図を書かなくてもたすき掛けができてしまうんですよ。
うさこ
私にはまだ早いかもしれません…
パン太先生
慣れたら参考までにやってみるくらいの気持ちでいいですよ。大したことではありませんので。
パン太先生
手順は簡単です。
①\(a\) , \(c\) とかっこ( )だけ書いてしまいましょう。
②それっぽい \(bd\) の組み合わせを入れて内内外外で掛けて足して確かめましょう。
①\(a\) , \(c\) とかっこ( )だけ書いてしまいましょう。
②それっぽい \(bd\) の組み合わせを入れて内内外外で掛けて足して確かめましょう。
うさこ
どういうことですか?内内外外って??
パン太先生
では、先ほどの例で試してみましょう。
\(2x^2+7x+6\)
パン太先生
① \(a\) , \(c\) とかっこ( )だけ書いてしまいましょう。
\((2x\) \()(x\) \()\)
パン太先生
こんな感じです。次に
②それっぽい \(bd\) の組み合わせを入れて内内外外で掛けて足しましょう。
今回は \(6\) と \(1\) を入れてみましょう。
②それっぽい \(bd\) の組み合わせを入れて内内外外で掛けて足しましょう。
今回は \(6\) と \(1\) を入れてみましょう。
\((2x+6)(x+1)\)
パン太先生
ここで内内外外が出てきます。意味は内側と内側、外側と外側です。内側と内側を掛けて、外側と外側を掛けてそれを足します。\(2x×1\) , \(6×x\) です。それを足してください。
\((2x×1)+(6×x)=8x\)
パン太先生
ここで出た値が与えられた式の2項目であればよいのです。今回の場合は \(7x\) であれば当たりです。先ほどもこの組み合わせは間違いでしたね。
うさこ
さっき当たりだった \(3\) と \(2\) の組み合わせでやってみます!まず手順①ですね!
\((2x\) \()(x\) \()\)
うさこ
そして手順②っと…
\((2x+3)(x+2)\)
\((2x×2)+(3×x)=7x\)
うさこ
先生できました!!
パン太先生
素晴らしいですね。少しでも手間を省きたい人は試してみてくださいね。


