文字を含むたすき掛けの方法

パン太先生

文字を含んでいたとしてもすでに学習しているたすき掛けと基本的には変わりません。たすき掛けの基本のページを学んでからこのページを見ることをおすすめします。

パン太先生

まずはじめにたすき掛けの基本をおさらいしましょう。たすき掛けを使う公式とやり方は次の通りでしたね。

公式　\(acx^2+(ad+bc)x+bd=(ax+b)(cx+d)\)

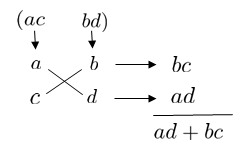
パン太先生

\(ac\) と \(bd\) の組み合わせを見つけて上の図のようにたすき掛けをするんでしたね。内側と内側、外側と外側を掛けてそれを足すという説明もしました。

パン太先生

それでは例を出して説明します。

例1）  \(ax^2-(a^2-2)x-2a\)

パン太先生

\(a\) と \(c\) , \(b\) と \(d\) の組み合わせをたすき掛けしてみて、\(x\) の係数の \(-(a^2-2)\) になる組み合わせを探します。

うさこ

\(ac\) は \(a×1\)
\(bd\) は \(2×(-a)\) と \(-2×a\)
です。

パン太先生

ではさっきの図に当てはめてみましょう。因みにですが \(ac\) の組み合わせの符号はなるべく＋にしておきましょう。\(ac\) は1通りしかないので決まりです。

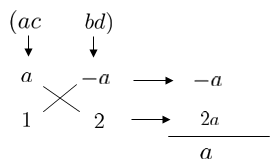
パン太先生

\(x\) の係数である \(-(a^2-2)\) になっていませんのでこれは違います。\(b\) と \(d\) を入れ替えてみましょう。

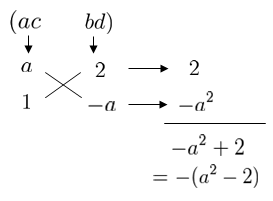
うさこ

これは \(x\) の係数と同じなので大丈夫ですよね？

パン太先生

そうですね。最後まで因数分解してください。

        \(ax^2-(a^2-2)x-2a\)
        \(=(ax+2)(x-a)\)

パン太先生

式が多少複雑になっても同じ方法で因数分解することができます。例2を見てください。

例2）  \((4a^2-b^2)x^2-8abx-(4a^2-b^2)\)

パン太先生

さて、この問題もたすき掛けしてみましょう。

うさこ

まずは \(ac\) と \(bd\) をつくったら良さそうですね。

        \((4a^2-b^2)x^2-8abx-(4a^2-b^2)\)
        \(=(2a+b)(2a-b)x^2-8abx-(2a+b)(2a-b)\)

うさこ

あとはたすき掛けをするだけですね！

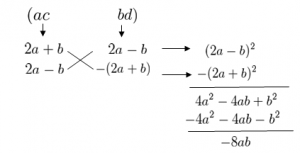
パン太先生

たすき掛けはこうなりますね。因数分解を最後までやってみましょう。

        \((2a+b)(2a-b)x^2-8abx-(2a+b)(2a-b)\)
        \(=\{(2a+b)x+(2a-b)\}\{(2a-b)x-(2a+b)\}\)
        \(=(2ax+bx+2a-b)(2ax-bx-2a-b)\)

パン太先生

式が多少複雑になっても基本的なたすき掛けができると問題なく因数分解ができますので、しっかり練習しましょう。