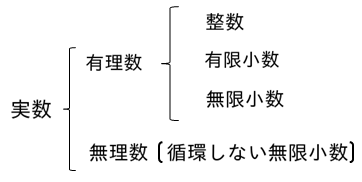
実数とその分類
実数
パン太先生
今回は実数とその分類について勉強します。実数や有理数、無理数などの用語が出てきます。しっかりと分類できるよう頑張っていきましょう。
うさこ
はい!頑張ります!さっそく実数について教えてください。
パン太先生
実数とは数直線上で表すことのできる数のことをいいます。後に複素数という数が出てきますが、それを知らない今の段階ではあなたの知っている数すべてが実数と考えても構いません。
実数…数直線上で表すことのできる数
パン太先生
そして実数は有理数と無理数に分類されます。
有理数と無理数
パン太先生
有理数とは、整数 \(a\) と \(0\) でない整数 \(b\) を使って、分数 \(\frac {a}{b}\) の形に表される数のことをいいます。例えば次のような数です。
例)\(\pm 2\) , \(\frac {1}{2}=0.5\) , \(\frac {1}{3}=0.333\dots\)
うさこ
なぜ \(b\) は \(0\) じゃだめなんですか?
パン太先生
数学では \(0\) で割るというのが許されていないからです。そういう決まりがあると覚えておいてください。
うさこ
そうなんですか!覚えておきます。
パン太先生
次に無理数です。無理数とは整数 \(a\) と \(0\) でない整数 \(b\) を使って、分数 \(\frac {a}{b}\) の形に表すことのできない数のことをいいます。これは循環しない無限小数と覚えても同じことです。例えば次のような数です。
例)\(\sqrt {2}=1.4142\dots\) , \(\pi=3.14159\dots\)
うさこ
確かに循環はしていないですね。
パン太先生
有理数と無理数について簡単にまとめます。
有理数…整数 \(a\) と \(0\) でない整数 \(b\) を使って、分数 \(\frac {a}{b}\) の形に表される数
無理数…整数 \(a\) と \(0\) でない整数 \(b\) を使って、分数 \(\frac {a}{b}\) の形に表すことのできない数(循環しない無限小数)
パン太先生
そして有理数は、整数、有限小数、循環小数に分けることができます。
整数・有限小数・循環整数
パン太先生
整数とは、\(0\) から \(1\) ずつ増やすか減らすかしてできる数のことをいいます。例えば次のような数です。
例)\(0\) , \(\pm 1\) , \(\pm 2\) , \(\pm 3\)
うさこ
これはなじみ深いですね。
パン太先生
次に有限小数とは、\(1.5\) のように有限で終わる小数を有限小数といいます。
例)\(\frac {1}{2}=0.5\) , \(\frac {1}{4}=0.25\)
パン太先生
循環小数とは \(0.33\dots\) のように同じ数字の列が繰り返されてる小数です。
例)\(0.585858\dots\)
パン太先生
では簡単にまとめておきましょう。
整数 …\(0\) から \(1\) ずつ増やすか減らすかしてできる数
有限小数…有限で終わる小数
循環小数…ある桁から先で同じ数字の列が無限に繰り返される小数
実数の分類(まとめ)
パン太先生
ここまで勉強して数にはたくさんの種類があることが分かりましたね。それでは最後に実数の分類を表にまとめて終わりましょう。
●実数の分類