循環小数の問題
分数を小数の形にする問題
パン太先生
今回は循環小数について勉強します。まずは分数を小数の形にする問題を勉強しましょう。循環小数を求める際は次の点に注意しましょう。
①実際に割り算を行う
②循環する部分が2回以上出るまで行う
③循環する最初と最後の数の上に・をつける
②循環する部分が2回以上出るまで行う
③循環する最初と最後の数の上に・をつける
パン太先生
この決まりを守って例題をやってみましょう。
例1) \(\frac {15}{11}\)
パン太先生
実際に割り算を(①)循環する部分が2回以上出るまで(②)やってみましょう。
\(\frac {15}{11}\)\(=1.363636\dots\)
パン太先生
②までできたら、循環する最初と最後の数の上に・をつけましょう(③)。この場合は \(3\) と \(6\) が循環していているので \(3\) と \(6\) に点をつけます。
\(\frac {15}{11}\)\(=1.363636\dots\)
\(=1.\dot {3}\dot {6}\)
\(=1.\dot {3}\dot {6}\)
パン太先生
この要領でもう1題やってみましょう。
例2) \(\frac {1}{37}\)
パン太先生
手順通りやってみましょう。
\(\frac {1}{37}\)\(=0.027027\dots\)
パン太先生
循環している数字はなんですか?
うさこ
\(027\) が循環しています。最初と最後の数の上に・をつけるので、\(0\) と \(7\) に・をつければいいんですね。
パン太先生
その通りです。
\(\frac {1}{37}\)\(=0.027027\dots\)
\(=0.\dot {0}2\dot {7}\)
うさこ
出来ました!
パン太先生
では次は循環小数を分数になおす方法を勉強しましょう。
循環小数を分数にする問題
パン太先生
さっきは分数を循環小数にする問題を勉強しました。その逆も可能です。次は循環小数を分数にする方法を勉強しましょう。
うさこ
見ただけではどんな分数になるか見当がつきませんよ。
パン太先生
安心してください。これにもやり方がありますので、手順を確認しましょう。
①問題の循環小数を \(x\) とおく
②循環する桁数 \(a\) のとき \(10^ax\) をとる
③\(10^ax-x\) を筆算する
②循環する桁数 \(a\) のとき \(10^ax\) をとる
③\(10^ax-x\) を筆算する
パン太先生
それでは実際に例を見ていきましょう。
例1) \(0.\dot {1}\dot {2}\)
パン太先生
まずは循環小数を \(x\) とおきます。
\(x=0.\dot {1}\dot {2}\)
パン太先生
循環する桁数はいくつですか?
うさこ
\(1\) と \(2\) の2桁です。
パン太先生
それでは \(10^2x=100x\) をつくりましょう。
\(100x=12.1212\dots\)
うさこ
あとは \(100x-x\) を筆算で行えばいいんですね?
パン太先生
そうですね、筆算してみましょう。
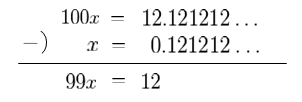
うさこ
小数点以下が同じように循環しているのできれいになくなるんですね!
パン太先生
よく気が付きました。これで整数にすることができましたね。あとは方程式を解いて分数の形にしましょう。
\(99x=12\)
\(x=\)\(\frac {12}{99}\)
\(=\)\(\frac {4}{33}\)
\(x=\)\(\frac {12}{99}\)
\(=\)\(\frac {4}{33}\)
パン太先生
約分ができるときは必ず約分をしましょう。また、これ以上約分できない分数を既約分数というので覚えておきましょう。
パン太先生
ではもう1問練習しましょう。
例2) \(1.\dot {5}6\dot {7}\)
パン太先生
さっき勉強した手順通りにやってみましょう。
うさこ
まず循環小数を \(x\) において、
\(x=1.\dot {5}6\dot {7}\)
うさこ
循環しているのは \(5,6,7\) の3桁だから \(10^3x=1000x\) をつくる、
\(1000x=1567.567567\dots\)
うさこ
これの差を筆算すると、
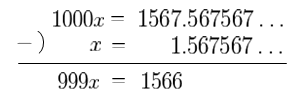
うさこ
あとは方程式を解いて、既約分数にして完了ですね。
\(999x=1566\)
\(x=\)\(\frac {1566}{999}\)
\(=\)\(\frac {58}{37}\)
\(x=\)\(\frac {1566}{999}\)
\(=\)\(\frac {58}{37}\)
パン太先生
よく最後までできました。決して難しいことはないのでしっかり練習しましょう。


